Introduction 

The purpose of this example is the optimization of the MOP2 multi-objective test function. This function first appeared in the following paper:

C. M. Fonseca and P. J. Fleming, “Multiobjective genetic algorithms made easy: Selection, sharing and mating restriction,” Genetic Algorithms in Engineering Systems: Innovations and Applications, pp. 45–52, Sep. 1995. IEE.

Definition

The MOP2 function is defined for an arbitrary number ${n}$ of design variables as follows:

Minimize ${f_1}$, ${f_2}$, where:

\[{f_1}\left( {{x_1},{x_2},...,{x_n}} \right) = 1 - \exp \left( { - \sum\limits_{i = 1}^n {{{\left( {{x_i} - \frac{1}{{\sqrt n }}} \right)}^2}} } \right)\]

\[{f_2}\left( {{x_1},{x_2},...,{x_n}} \right) = 1 - \exp \left( { - \sum\limits_{i = 1}^n {{{\left( {{x_i} + \frac{1}{{\sqrt n }}} \right)}^2}} } \right)\]

Due to the mathematical formulation of the function, the minimum for function ${f_1}$ is located at:

\[\left( {{x_1},{x_2},...,{x_n}} \right) = \left( {\frac{1}{{\sqrt n }},\frac{1}{{\sqrt n }},...,\frac{1}{{\sqrt n }}} \right)\],

while the minimum for function ${f_2}$ is located at:

\[\left( {{x_1},{x_2},...,{x_n}} \right) = \left( { - \frac{1}{{\sqrt n }}, - \frac{1}{{\sqrt n }},..., - \frac{1}{{\sqrt n }}} \right)\].

Due to the symmetry of the problem, the Pareto-optimal is given for all points in the line defined by:

\[{x_1} = {x_2} = ... = {x_n} \wedge  - \frac{1}{{\sqrt n }} \le {x_1} \le \frac{1}{{\sqrt n }}\]. 

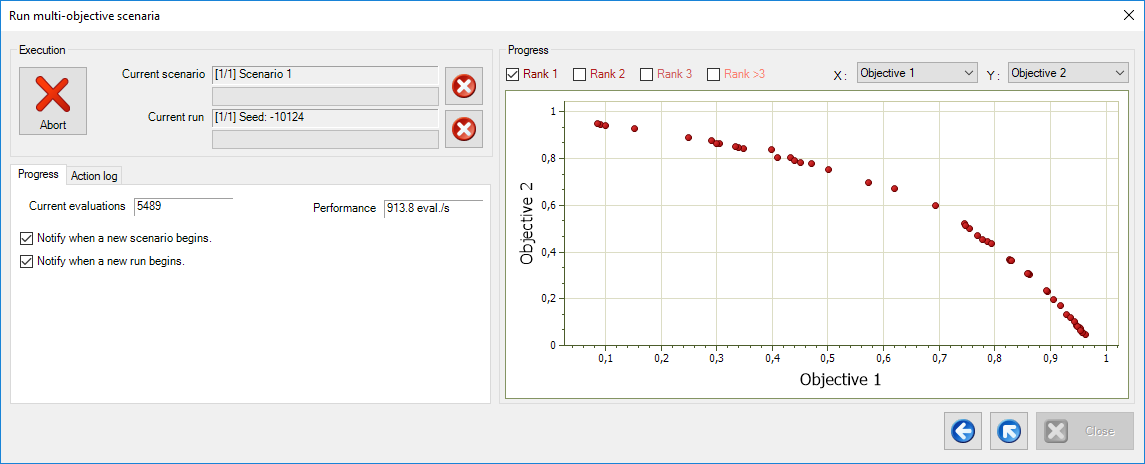
Setting up and solving the problem is very simple. The file for this example can be found here. In the ribbon of xlOptimizer, just click on the Run multi-objective button, and then click on the Run button in the form that appears.